In mathematics, the concept of a curve tries to capture the intuitive idea of a geometrical one-dimensional and continuous object. A simple example is the circle. In everyday use of the term "curve", a straight line is not curved, but in mathematical parlance curves include straight lines and line segments. A large number of other curves have been studied in geometry.
This article is about the general theory. The term curve is also used in ways making it almost synonymous with mathematical function (as in learning curve), or graph of a function (Phillips curve).

Definitions
The distinction between a curve and its image is important. Two distinct curves may have the same image. For example, a line segment can be traced out at different speeds, or a circle can be traversed a different number of times. Many times, however, we are just interested in the image of the curve. It is important to pay attention to context and convention in reading.
Terminology is also not uniform. Often, topologists use the term "path" for what we are calling a curve, and "curve" for what we are calling the image of a curve. The term "curve" is more common in vector calculus and differential geometry.

Conventions and terminology
Main article: arc length
If X is a metric space with metric d, then we can define the length of a curve
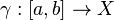
A rectifiable curve is a curve with finite length. A parametrization of is called natural (or unit speed or parametrised by arc length) if for any t₁, t₂ in [a,b], we have
If is a Lipschitz-continuous function, then it is automatically rectifiable. Moreover, in this case, one can define speed of at t₀ as

and then

In particular, if is Euclidean space and 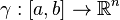differentiable then


Lengths of curves

Main article: differential geometry of curves Differential geometry

Main article: Algebraic curve